Scaling Test Time Inference for Protein Language Models

Justin Jung1

1 Biohub

Code

TL;DR

We investigate test time inference scaling for protein language models under different generation search and sampling strategies. We benchmark on the ESM3 1.4B Open model and consider both unconditional structure generation quality (pTM) of various sequence lengths and challenging tertiary coordination scaffold design generation.

Test Time Scaling

Best-of-N Inference Scaling

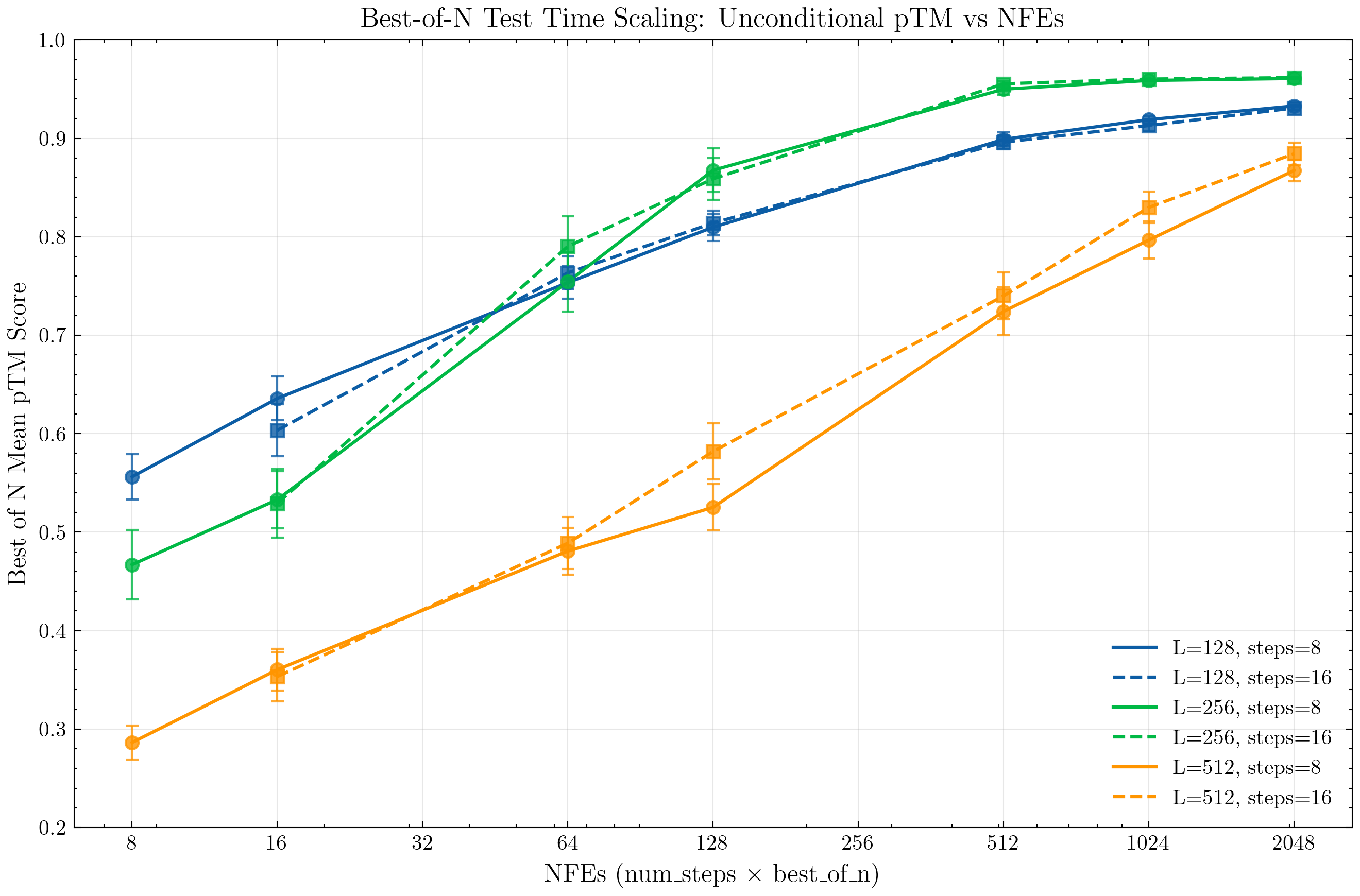
First, we establish general trendlines of unconditional joint sequence and structure generation quality as we scale inference compute. Sequences are generated with a temperature of 0.7, prompted with a fully masked sequence of length 128 or 256. Structures are generated using the default configuration temperature 1.

For evaluation, we compute the mean "Best-of-N" pTM generation score over a sample of 128 generated structures.

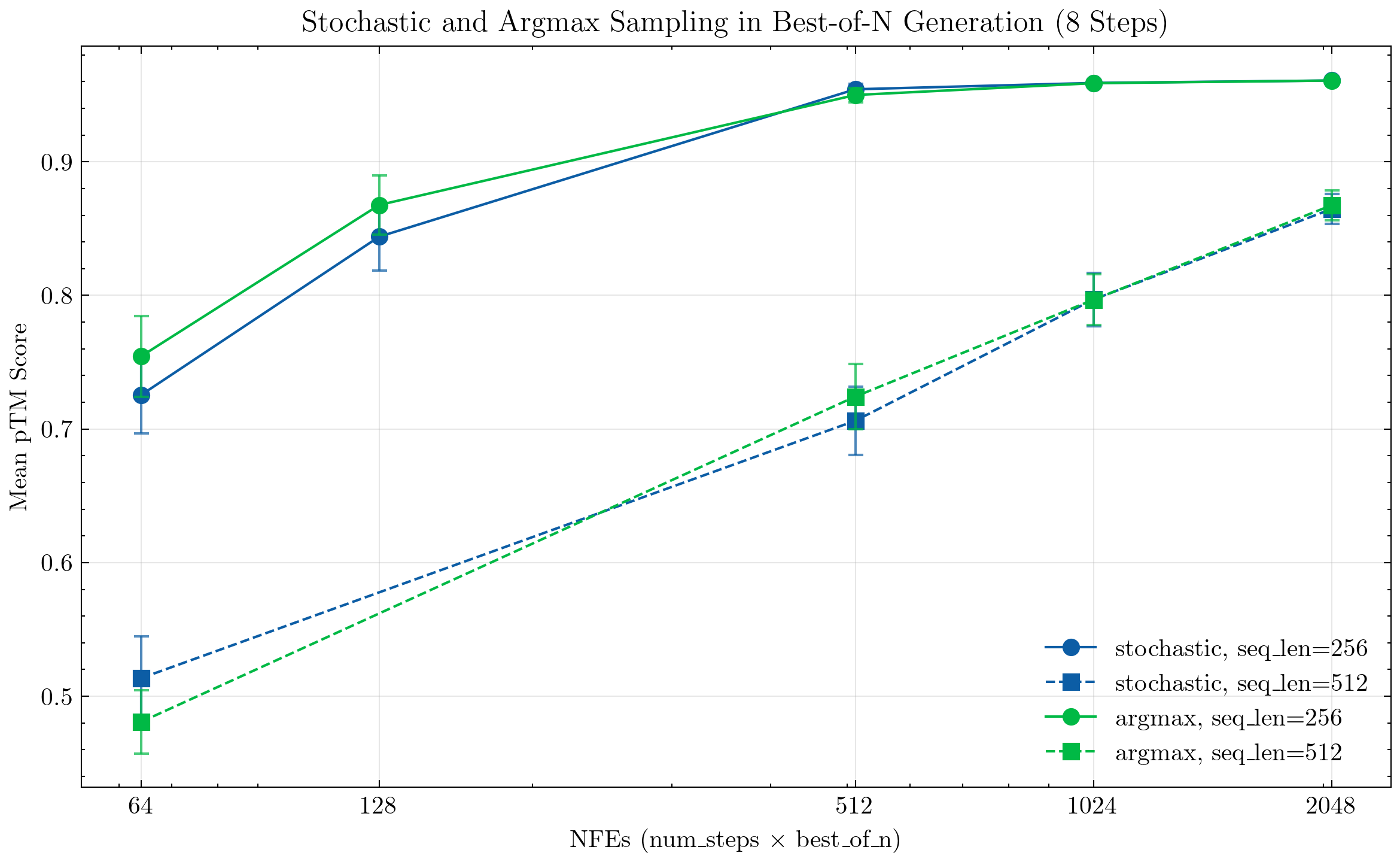
Best-of-N scaling
Figure 1: Best-of-N unconditional generation pTM score under varying number of NFEs.

Stochastic vs Argmax Sequence Generation

The current ESM3 model utilizes a deterministic logit argmax token decoding strategy which significantly limits diversity of generated sequences/structures. We instead consider softmax stochastic sampling (sampling a multinomial distribution defined by the logit softmax values) as done in MaskGIT and discrete diffusion. We find that the generation quality of stochastic sampling is similar to the deterministic argmax sampling. From here on all experimental results use the stochastic sampling setting.

Best-of-N scaling
Figure 2: Stochastic vs Argmax Sampling unconditional generation (sequence length 256) pTM score under varying number of NFEs (and varying best of N).

Tertiary Coordination Scaffold Design Task

We adapt the tertiary coordination scaffold design task as detailed in the appendix section (A.4.5) of Hayes et al. (2025). We design the protein sequence prompt by providing the coordinating residues in the order and location as in the original sequence while masking out the rest, where the prompt sequence length is the length of the original full protein sequence.

To eliminate variability in protein generation quality due to sub-optimal folding, for each sequence we generate 16 folds and return the highest pTM fold. We find that best fold out of a set of 16 or 32 empirically have low variance in pTM score and well saturate the gains of increasing the number of folds.

We use one of the listed coordinating ligands (PDB ID 8gxp) and the coordinating residues as in (A.4.5).

We get an estimate for the model success rate in generating a scaffold in this coordination task, where we define a successs by a generated structure with pTM > 0.8 and rMSD < 2.0. Specifically, we estimate the success rate using 3,500 generations (using n=8 steps for sequence generation, n=32 steps and best-of-16 for structure generation) and find a estimated success rate of p = 0.0571%, confirming the difficulty of this design task.

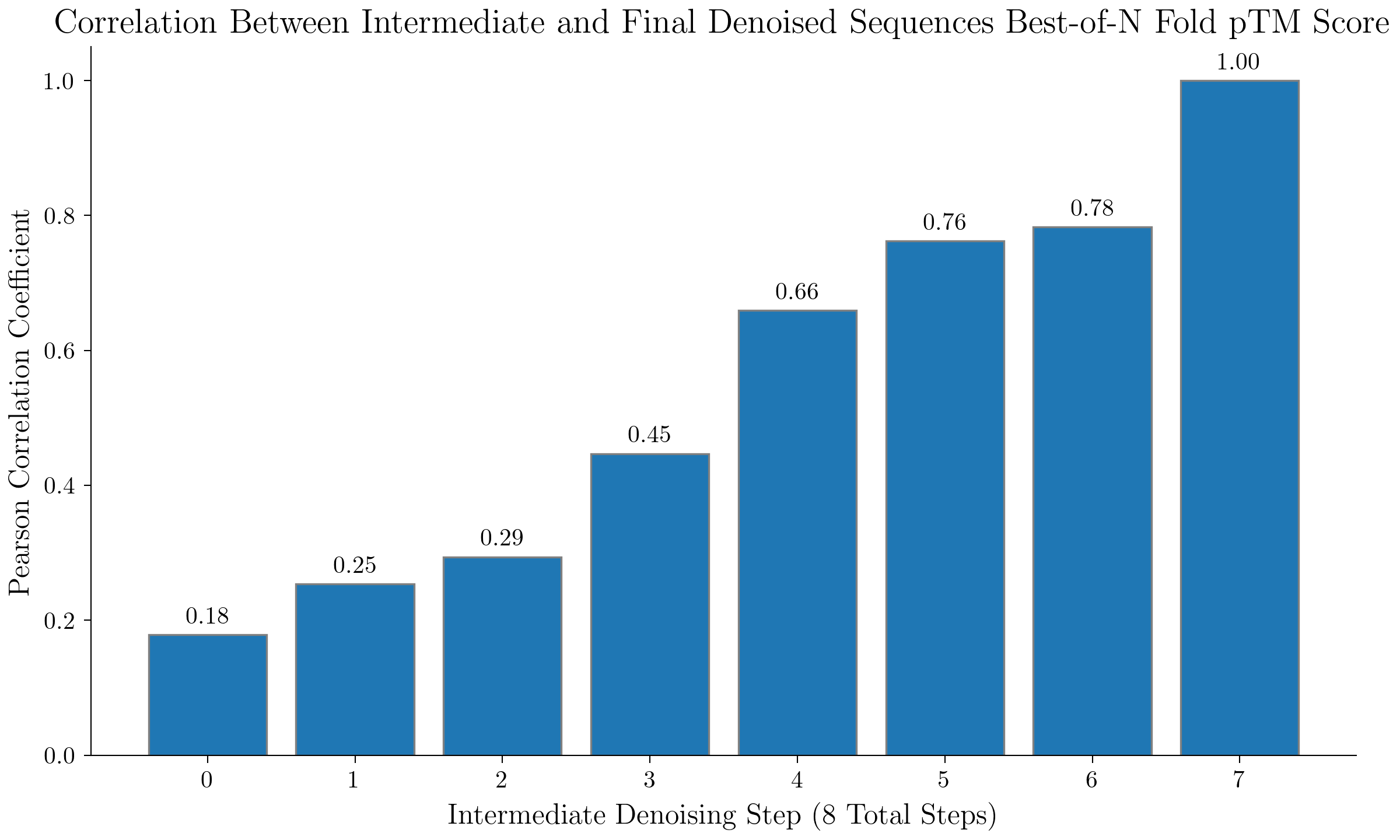
Value Estimates via Intermediate Denoised Sequences

We analyze how well pTM scores of intermediate denoised estimates of the final sequence (obtained by using all of the denoised logits at some intermediate timestep) track with the actual final generated sequence pTM score. For our generation prompt, we use the coordinating ligand prompt as above and we get a pTM score via the best pTM score out of a set of 16 folds for a given generated sequence.

We see a strong correlation between the intermediate denoised estimate sequence scores and the final sequence scores, motivating the use of intermediate estimated scores in test time search (ex: beam search).

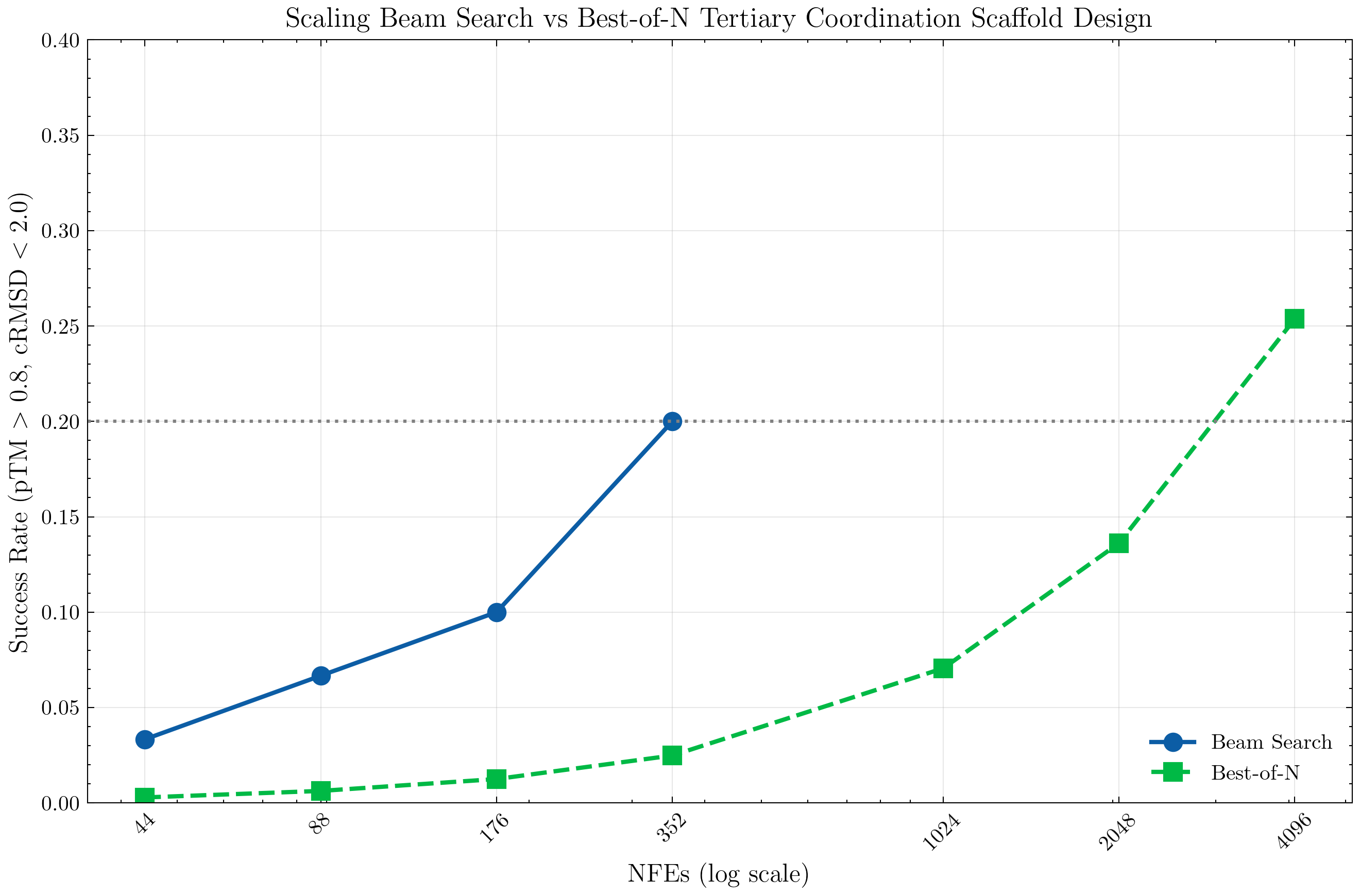
Best-of-N scaling
Figure 3: Pearson correlation between intermediate and final denoised sequence pTM score (evaluated on 8gxp ligand coordination task with n=8 steps for sequence generation). Correlation calculated using 156 sequence generations.

Best-of-N Baseline Success Rates

Given our estimated success rate of p = 0.0571%, we can calculate the expected success rate of a Best-of-8 generation.

Specifically, we get that the probability of success is:

p_8 = 1-(1-p)^8 = 0.456%

and with n=8 timesteps each Best-of-8 generation takes a total of 64 NFEs.

Beam Search Success Rates

Given our correlating intermediate value signal, we can utilize a strategy such as beam search as an improvement over Best-of-N sampling.

Here, we have two variables of interest, pTM and rMSD score, and so we define a scoring function that penalizes outliers via an exponential:

L(p, r) = e^{-5(p - 0.8)} + e^{0.5(r - 2.0)}

where our scoring function is the negative of the loss.

After looking at the intermediate signal correlations, we decide to only utilize the intermediate value signal after the first four denoising steps. Specifically, for the first 4 steps, we simply do independent parallel generation of 8 sequences, as in best-of-n generation.

Then, we employ beam search, where for each candidate node we generate four children nodes. We vary the number of NFEs by varying the beam search width, sweeping over width in [1, 2, 4, 8], leading to [44, 88, 176, 352] NFEs respectively.

By integrating intermediate rewards with beam search, we get a significantly higher success rate in comparison to brute force sampling. Notably, beam search achieves better performance than Best-of-n with an order of magnitude less samples. (We note that we estimate best-of-n success rate as above; we estimate the beam search success rate via the average over 60 generations.)

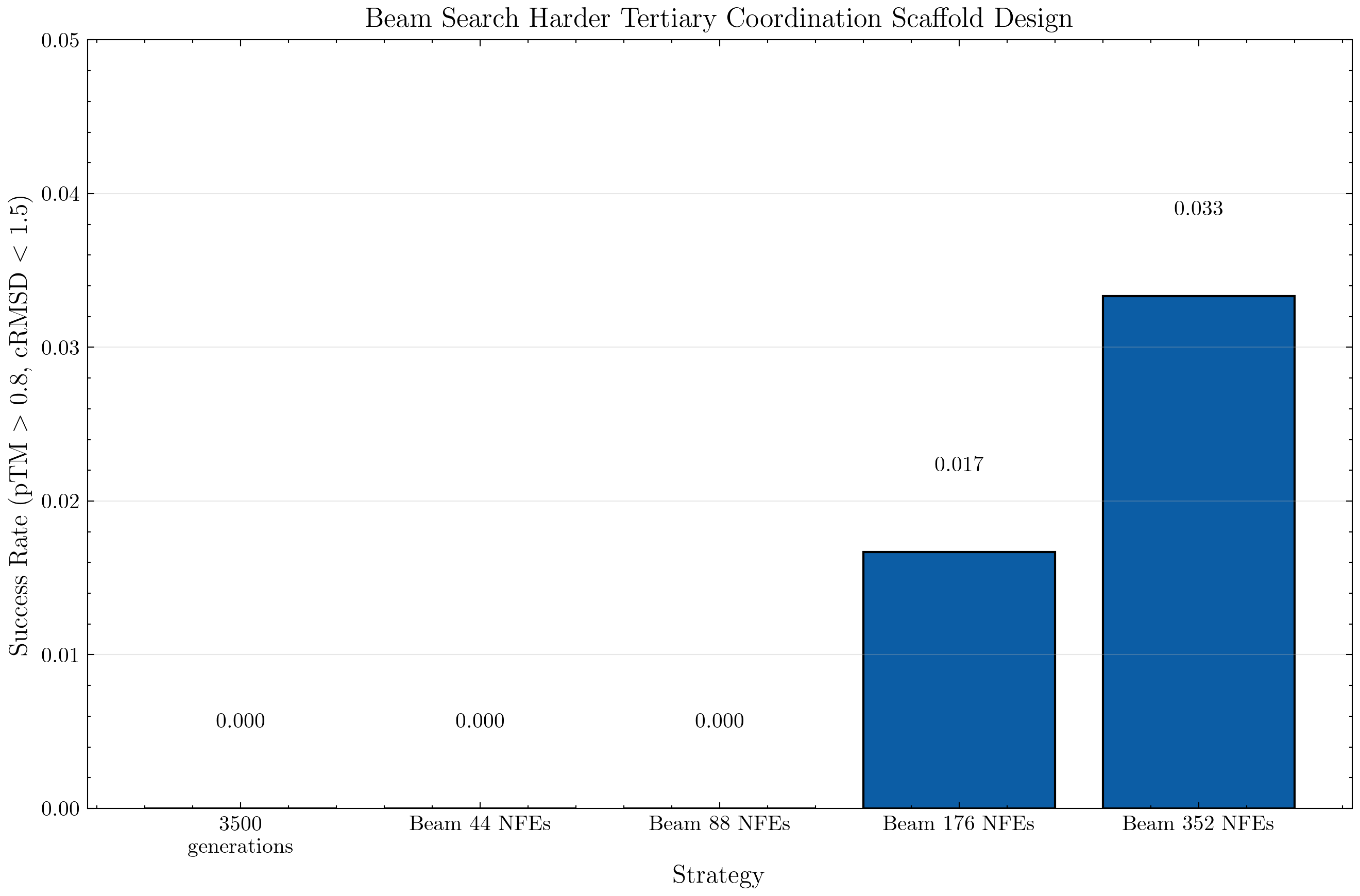
Best-of-N scaling
Figure 4: Beam Search vs Best-of-N tertiary coordination scaffold design success rate, where a success is defined by a pTM > 0.8 and rMSD < 2.0. Beam search success rate estimate calculated using 60 generated samples.

Moreover, we get evidence that simply scaling the number of generations may not be enough. For example, when we consider the harder tertiary scaffold task requirement of pTM > 0.8 and rMSD < 1.5, we note that with 3500 generations from the model (no search) we found zero that met the requirement.

However, the beam search strategy that integrated intermediate lookahead value estimates was able to do so for 176 and 352 NFEs.

Best-of-N scaling
Figure 4: Beam Search solves a more difficult tertiary coordination scaffold design task, where a success is defined by a pTM > 0.8 and rMSD < 1.5, whereas there are zero successes in 3500 generations. Beam search success rate estimate calculated using 60 generated samples.

References

Additional Experiments

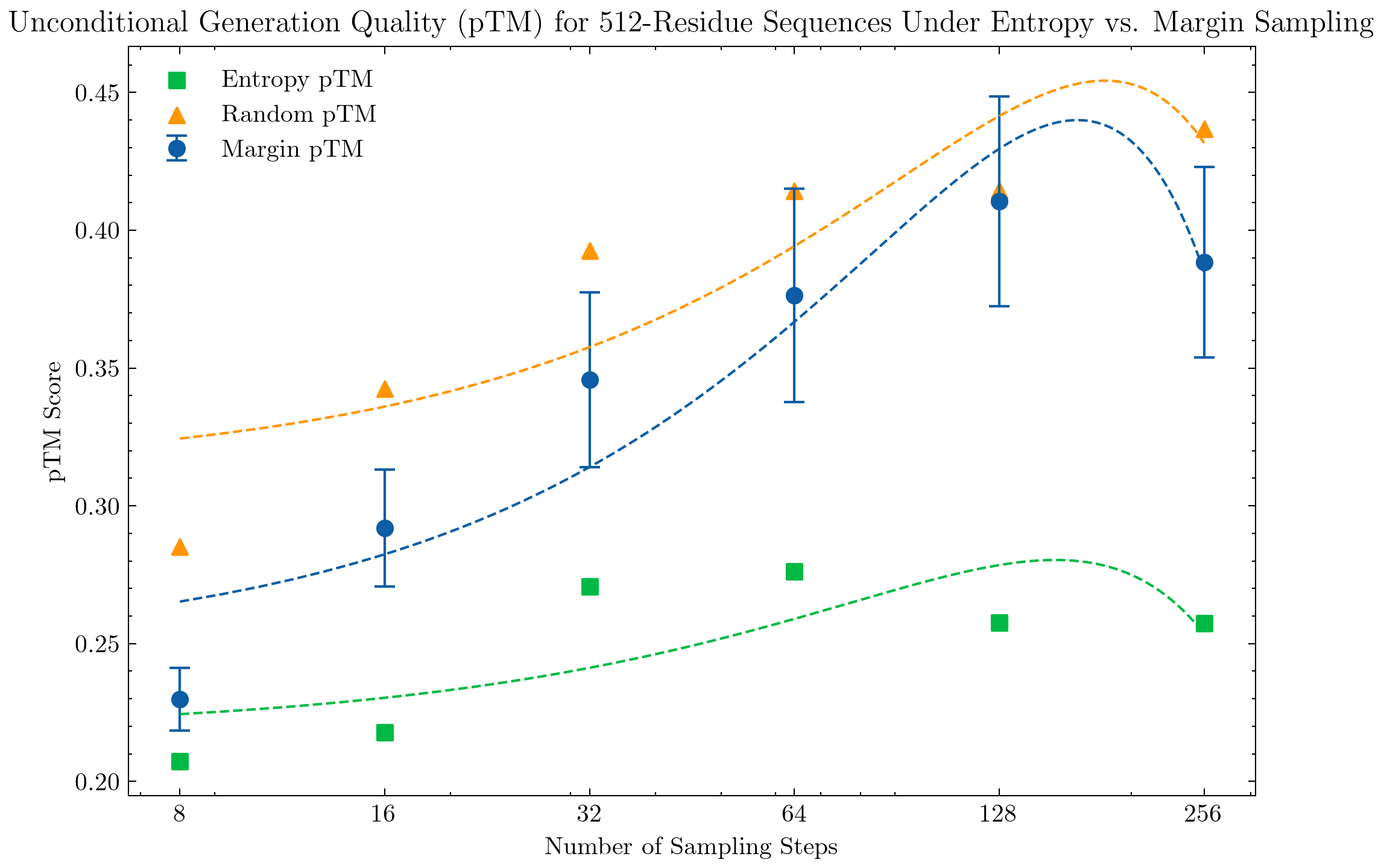
We research the impact of sampling strategies on generation quality. By default, ESM3 open offers both "entropy" and "random" sampling strategies, where entropy selects the top-k best token indices ranked by lowest entropy value, and random selects indices uniformly.

Prior work by Ye et al. (2024) demonstrates strong performance of discrete diffusion models on reasoning tasks and shows that top-k sampling (unmasking token indices with the highest logit values) outperforms random sampling. Kim et al. (2025) introduce the top probability margin strategy and show significant improvements on reasoning tasks.

We adopt this top probability margin approach, where the margin is defined as the difference between the model's two largest output probabilities (e.g probabilities of top two token indices i,j):

margin = |p_theta(x^i = j | x_t) - p_theta(x^i = i | x_t)|

and we select the top-K indices with the highest margins.

Sampling

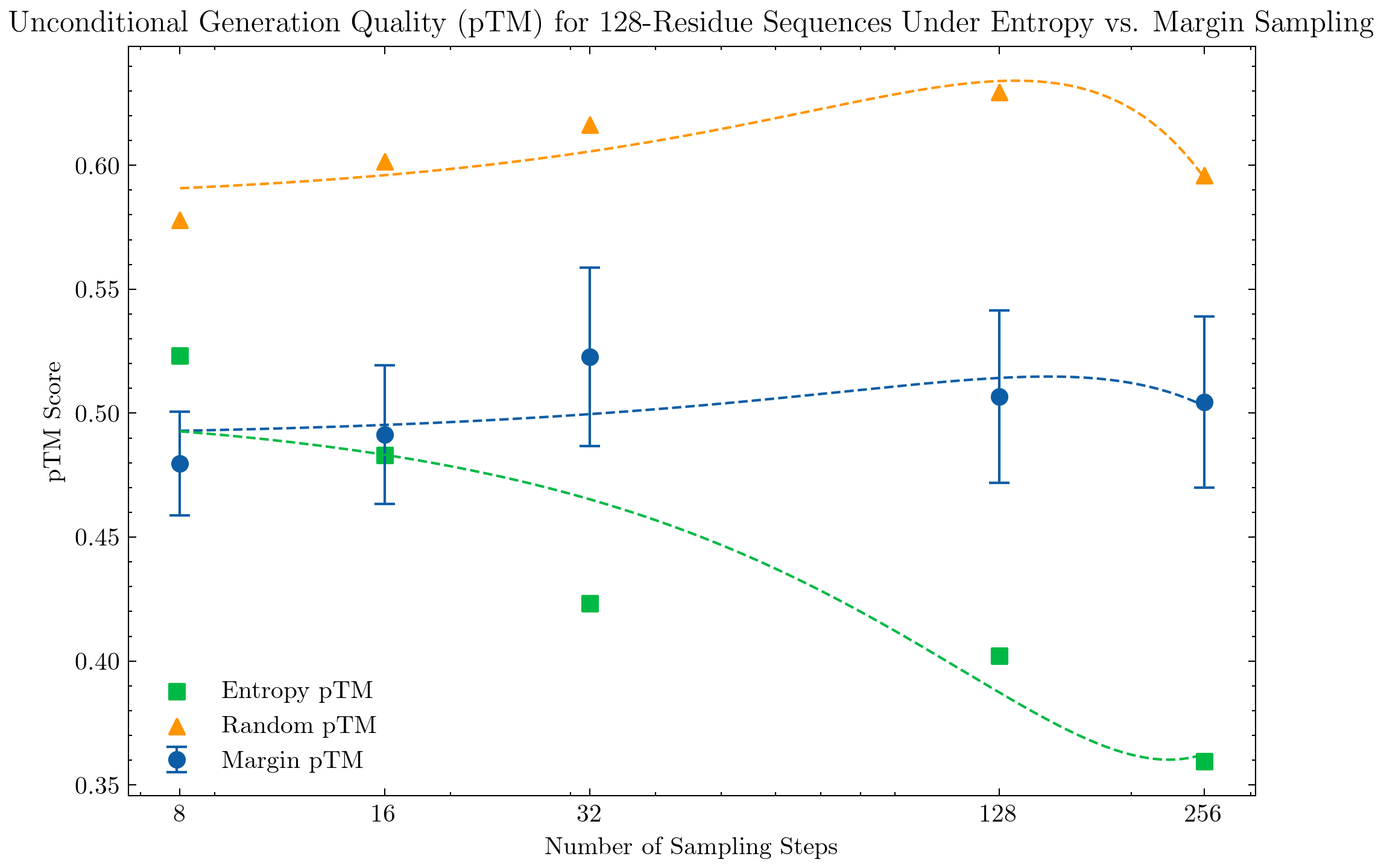
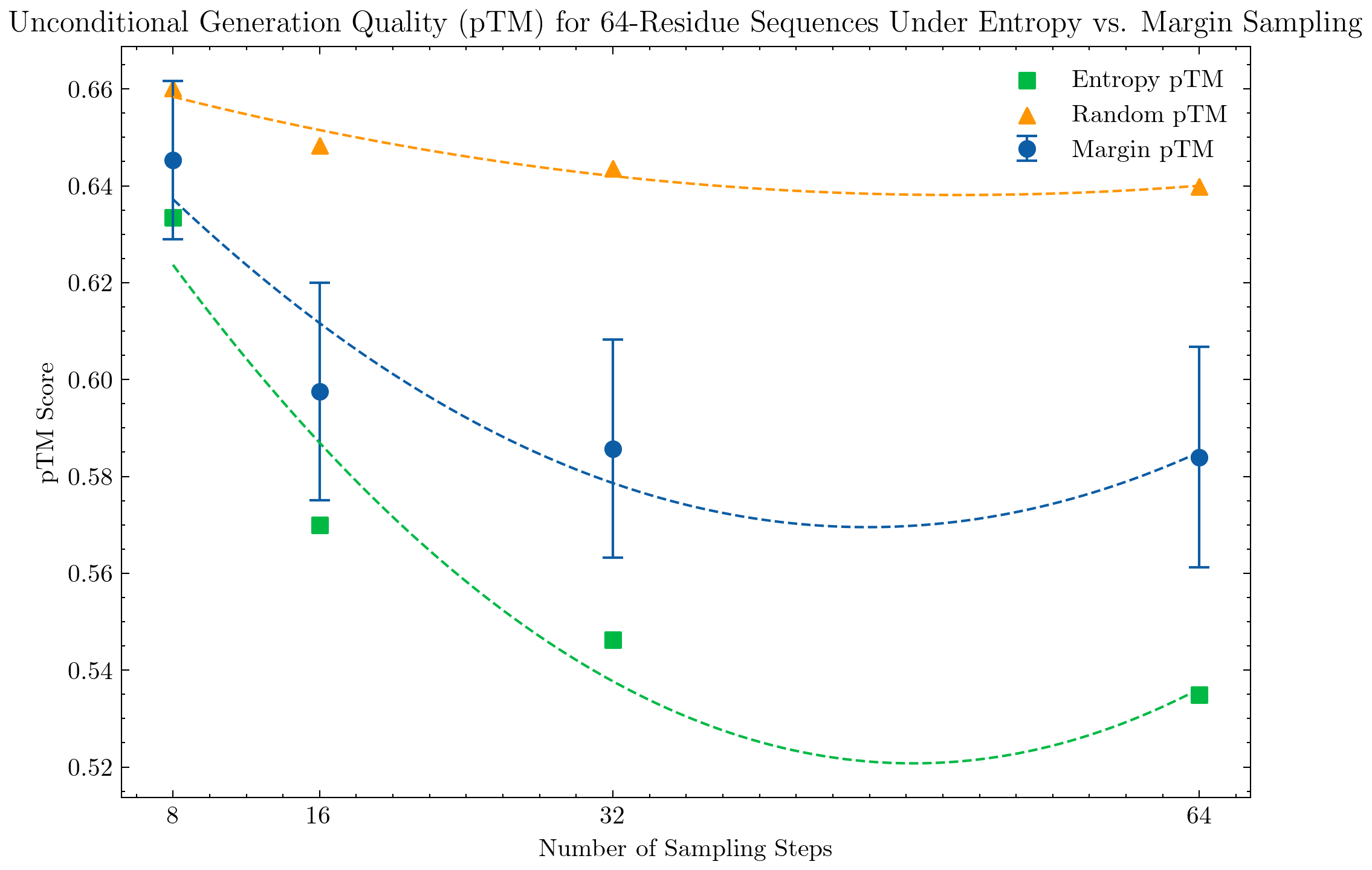
We evaluate unconditional sequence and structure generation under different sampling strategies. Sequences are generated with a temperature of 0.7, prompted with a fully masked sequence of length 64, 128, 256, or 512. Structures are generated using the default configuration temperature=1.

For evaluation, we compute the pTM score over a sample of 128 generated structures and report the mean score. For larger structures, we see a clear significant improvement under the top probability margin strategy in comparison to the top-k entropy strategy.

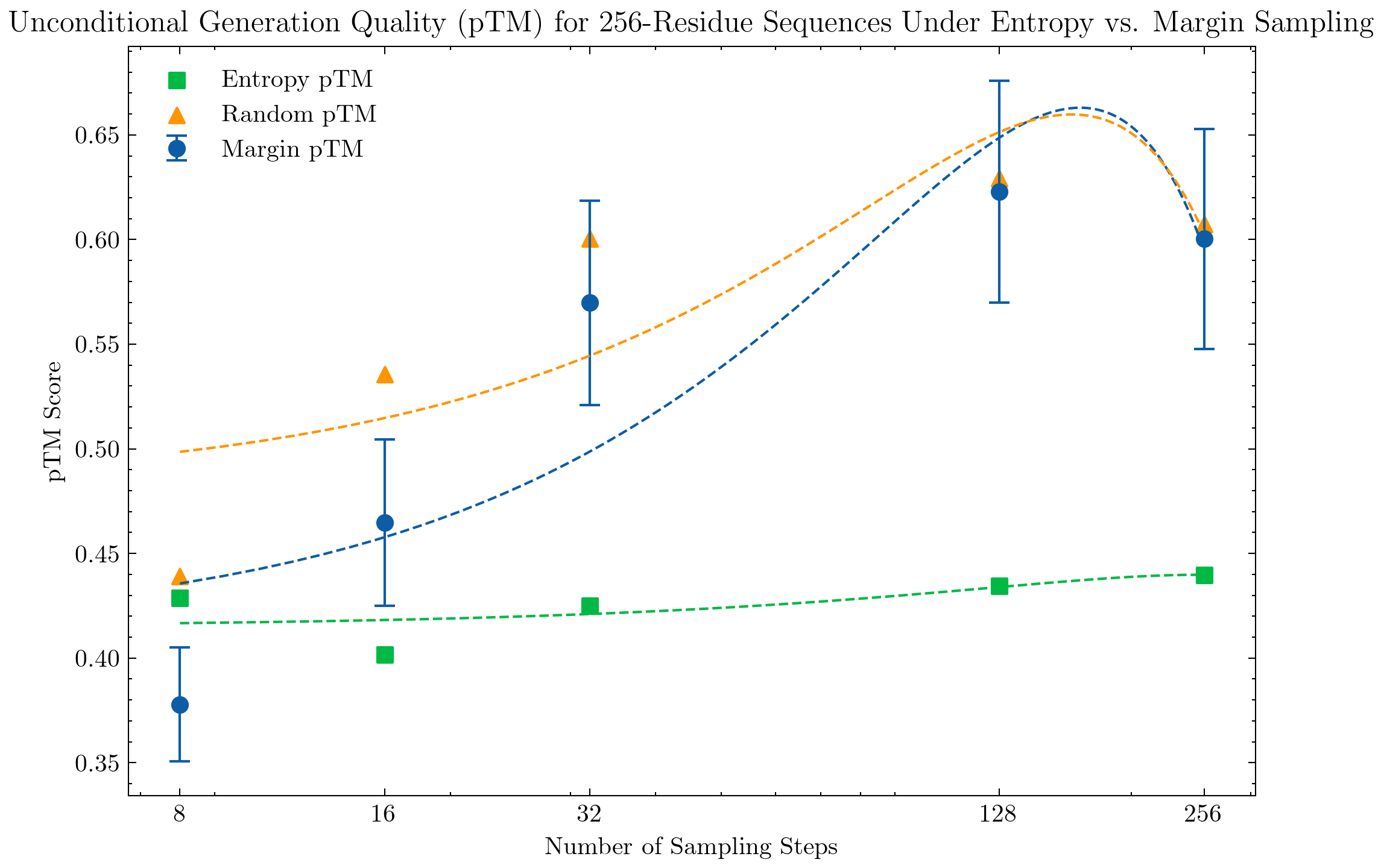
Best-of-N scaling
Figure 5: Unconditional generation (sequence length 256) pTM score under top-k entropy and top probability margin strategies across different sampling steps. Notably, the entropy strategy does not improve with increased number of sampling steps, whereas the margin strategy does, leading to a substantial difference in performance.

We see a similar evident performance boost with the top probability margin sampling strategy with unconditional generation of protein structures with 512 residues; we also interestingly see a similar performance trend of the top margin strategy across number of sampling steps, with 128 steps being most performant.

Best-of-N scaling
Figure 6: Unconditional generation (sequence length 512) pTM score under top-k entropy and top probability margin strategies.

We also evaluate the conditional generation of smaller protein structures, specifically structures with 128 and 64 residues. Interestingly, we do not see significant improvement under the margin strategy and the top-k entropy strategy performs well even with 8 steps.

Best-of-N scaling
Figure 7: Unconditional generation (sequence length 128) pTM score under top-k entropy and top probability margin strategies.
Best-of-N scaling
Figure 8: Unconditional generation (sequence length 64) pTM score under top-k entropy and top probability margin strategies.